Guided waves
Elastic guided waves (GW) are stress waves that propagate along an elongated structure (either plane or curvilinear) while guided by its boundaries. This allows the waves to travel a long distance with little loss in energy. For example, when a beam is excited at high frequency, stress waves travel in the beam along its axis away from the excitation source, i.e. the beam “guides” the waves along its axis. Similarly, in a plate, the two free surfaces of the plate “guide” the waves within its confines.
There are various application areas for guided elastic waves in solids, such as seismology, non-destructive evaluation, material characterization, delay lines, etc. Several classes of GW exist and a very important among these is that of Lamb waves (named after Sir Horace Lamb, who mathematically predicted their existence in 1917), which can propagate in a solid plate with free surfaces. Because of the abundance of plate and shell-like structural configurations, this class of GWs has been the subject of sufficient research efforts during the past two decades. Another class of GW modes is also possible in plates – the horizontally polarized shear or SH-modes. Other classes of GWs have also been examined in the literature. Among these are Rayleigh waves, which propagate close to the free surface of elastic solids, Love, Stoneley and Scholte waves that travel at material interfaces.
The exploitation of elastic GW for rapid inspection in non-destructive and structural health monitoring (SHM) applications is hindered by the need to overcome their considerable complication compared to conventional methods. At any chosen frequency there may exist at least two modes, so that the interaction of a wave with a defect can result in a complicated multimode signal. The modes travel at different speeds and are dispersive, which mean the dependence of their dispersion characteristics (e.g., wavelengths, phase and group velocities) from frequency:
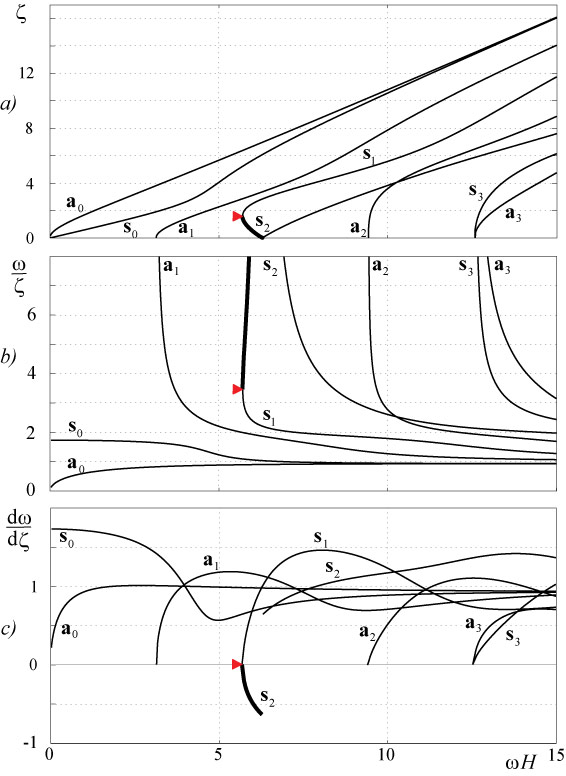
The latter results in strong changes of the multimode signal shape with distance while propagating along the plate. Also, the distributions of the stresses through the thickness of the plate differ from one mode to another and depends on frequency, thus the nature of the modes needs to be understood in order to choose modes which are sensitive to the defects. Anisotropy of mechanical properties of modern layered composite materials complicates GW propagation phenomenon sufficiently, making GW dispersion characteristics and amplitudes being dependent not only from frequency but from propagation direction as well. An example of GW patterns in unidirectional and cross-ply carbon-fiber reinforced laminates are shown in Fig. 2 (a and b respectively).


