Resonances
The effect of traveling wave blocking by a system of obstacles is widely used in various areas, such as vibrodamping, anti-seismic protection, opto- and microelectronics, etc. The effect manifests itself as deep gaps in the frequency spectra of transmitted signals. The gap band appearance is especially sound in periodic structures, e.g., with systems of interdigital contacts or grooves used in acoustoelectronic technology, in periodic composites, phononic lattices, and photonic crystals. On the other hand, a resonant shielding of traveling waves by one or more obstacles is known as a trapped mode effect. This effect features the capture and localization of time-averaged wave energy of a time-harmonic wave field in the form of energy vortices. The trapped mode effect is closely connected with the allocation of spectral points (poles) of the corresponding boundary value problem, which are natural frequencies of the waveguide with obstacles. The closer a pole is located to the real axis, the more the trapped mode effect becomes apparent. Besides the blocking ability, the resonance response of hidden defects can be used for nondestructive testing purposes, e.g., for guided wave crack and delamination detection in metallic and composite laminate plates.
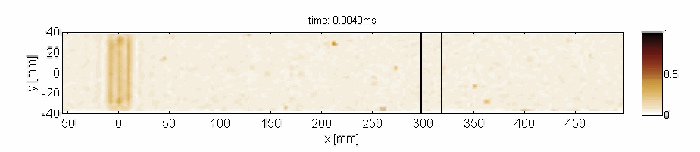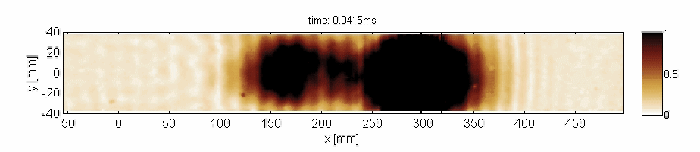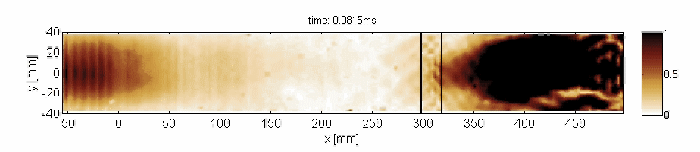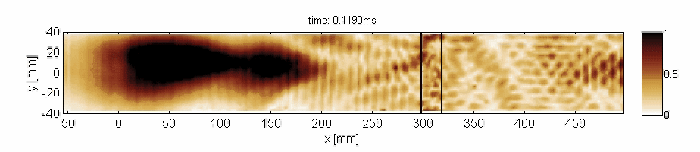
Non-resonant transmission of Lamb waves through the delaminated zone
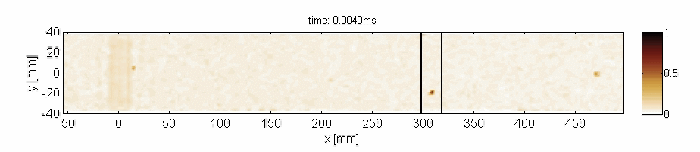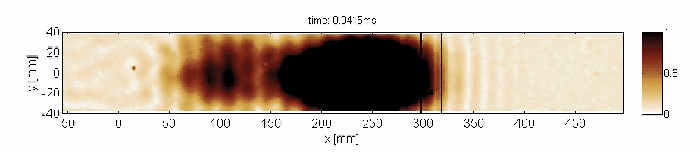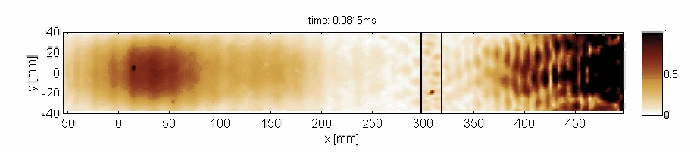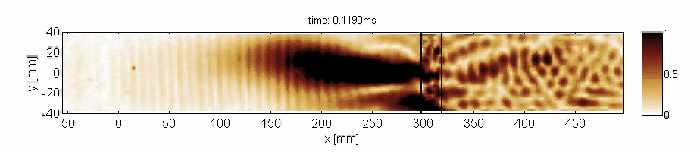
Capturing and localization of Lamb waves by crack
With several obstacles the number of natural frequencies increases in parallel with the number of defects. The location of the poles in the complex frequency plane depends on the defect’s relative position, but the gaps of transmission coefficient plots generally remain in the same frequency ranges as for every single obstacle separately. This property gives a possibility to extend gap bands by a properly selected combination of various scatterers. On the other hand, a resonance wave passing in narrow bands associated with the poles is also observed. Thus, while a resonance response of a single obstacle works as a blocker, the waveguide with several obstacles becomes opened in narrow vicinities of nearly real spectral poles, just as it is known for one-dimensional (1D) waveguides with a finite number of periodic scatterers.
Current activities of IMMI team in this field are concentrated on modeling guided wave interaction with 3D cracks and delaminations in isotropic metallic and anisotropic composite laminate plates, which includes development of efficient mathematical models and their computer implementation.